WIP Eta Carinae and the Carina Nebula images

 The following image is a work in progress set of narrowband images of the Carina Nebula (NGC 3372) taken with iTelescope T33 over three 30-minute sessions on 4/2/25, 4/425 and 4/5/25.

A standard Hubble SHO palette is used, so SII emission is red, H-alpha is green, and OIII emission is blue. No noise reduction other than the improved signal-to-noise afforded by image stacking (7x 3-minute H-alpha images, 6x 3-minute OIII images, and 9x 3-minute SII images).

 

More WIP AstroPhotography

After a long hiatus I've restarted effort on my own set of python tools for amateur astronomical data reduction. Here is a work in progress output from combining the very short set of SN 2023ixf images provied as part of the iTelesop Plan-20 Premium image set. Taken with iTelescope T24. 3x FITS images each of 300s Red, Green, Blue filter. iTelescope stock calibration, so there may be some residual bad pixels. Astrometric solution using Astromatic.net, and images realigned to North up, East to the left, with 0.62 arcseconds per pixel. Net exposure 15 minutes in each filter. RGB PNG generated by stiff, wavelet denoised in the gimp. Of course three images in each filter is much less data than needed for a serious product, but its ideal for testing my pipeline. Click to embiggen:

Work In Progress Astrophotography

Here are a few new amateur astronomical images I've been working on. These are very much a work in progress, in particular with handling the sky background when building up large mosiac images. These were taken using the iTelescope T05 (a 250mm Takahashi reflector) and T20 (a 106mm APO refractor) telescopes in New Mexico over a series of nights this year, and processed using various python tools I wrote for the purpose.

A 5x5 degrees SII, H-alpha and OIII mosaics of the Cygnus Loop supernova remnant, taken with T20. The struggle with the images were taken when the Moon was up, even though the were taken over several days. Weather has been crummy at the NM site this summer, so you make do with what you get. But the sky backgrounds need some additional work.

The other images are of the NGC 6888 (shown previously), and M82 and/or M81, each taken separately with T05, and mosaiced together in some versions. The depth of the different images and bands varies a lot, for example there are 25 5-minute H-alpha images of M82, but only 6 5-minute H-alpha images of M81. I also messed up by using the Johnson-Cousins B filter on M81 when I've used the Astrodon Blue on M82.

The Wolf-Rayet bubble NGC 6888

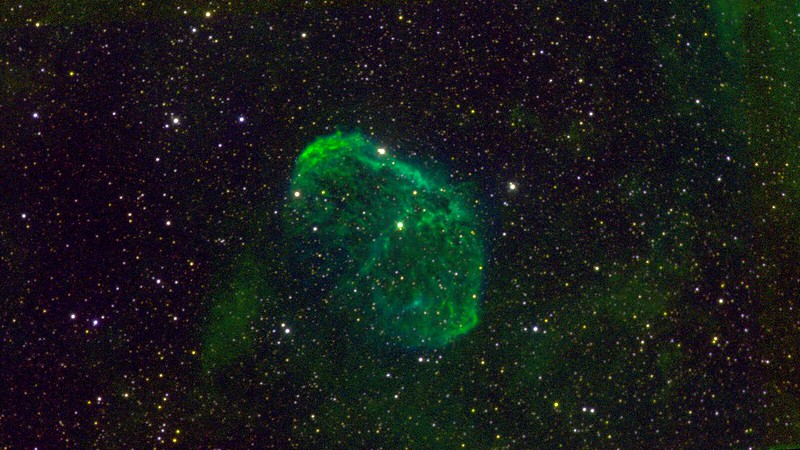
 As a bit of amateur astronomy I signed up with iTelescope in July 2020, and took some images of NGC 6888, a favorite object of mine. It took several months to accumulate the set of images I wanted, and another several months to write the tools to process the raw data in the way I wanted, but finally here they are:

NGC 6888 taken in SII (red), H-alpha (green) and OIII (blue) filters.

NGC 6888 using Astrodon Red, Green and Blue filters.

NGC 6888 is the wind blown bubble surrounding Wolf Rayet 136, at a distance of around 2,000 parsecs (6,500 light years) from us. WR 136 is an evolved massive star with a strong stellar wind (velocity approximately 1,500 km/s) that is blowing into the slower and denser ejecta from the star's previous Red Supergiant phase, creating a bubble approximately 10 pc x 7 pc in size (34 x 23 light years). WR 136 is the bright star at the center of the image. Although only about mV ~ 7.5, its intrinsic luminosity is approximately 500,000 times that of the Sun, and its effective temperature is 70 to 80 thousand degrees Kelvin,

The nebula emission seen in these images is almost exclusively swept-up and compressed RSG wind material, that has been photo-ionized by the WR star. The WR wind material inflating the bubble is shock-heated to million degree temperatures, and hence is not visible in these images. There are of course X-ray images of this hot gas, although the Chandra and XMM-Newton images only partly cover the bubble (given those observatories small field of view), and absorption from intervening interstellar gas and dust severely attenuates the soft X-ray emission. (I did a theoretical paper that modeled NGC 6888 as part of my PhD thesis work at the University of Birmingham back in the mid 1990's.)

The bubble itself is relatively young, at least compared to million-year-old main-sequence massive star wind bubbles and superbubbles: with an expansion velocity of approximately 80 km/s its dynamical age is only about 50,000 years. The relatively short lifespan of the RSG/WR wind interaction probably explains why WR bubbles are only clearly seen around a small fraction of galactic WR stars.

The hydro-dynamical instabilities caused by the interaction of the fast tenuous WR wind and the slow dense RSG wind are also the source of the beautiful substructure in the nebula, first demonstrated (I think) in some excellent papers by García-Segura and Mac Low in the mid 1990's [e.g. this paper]. They are even more apparent in the Hubble Space Telescope images of a small region of the rim of the bubble.

Telescope and image information:

• iTelescope T05 at New Mexico site (MPC H06)
• Takahashi Epsilon 250 with Paramount PME mount and SBIG ST-10XME CCD.
• Images taken on 2020-07-16, 2020-08-10, 2020-08-12, 2020-09-17 and 2020-10-16.
  
• Resampled images have 1.8 arcsecond square pixels aligned North at the top, East at the left, and cover a 0.96 degree x 0.54 degree FOV.
• Net exposure time:
• SII/H-alpha/OIII image: 113 minutes
  
• Red/Green/Blue image: 18 minutes
  
• Individual raw frames:
• SII/H-alpha/OIII image: SII 2x240s, 8x300s; H-alpha 9x180s; OIII 2x240s, 6x300s.
  
• Red/Green/Blue image: Red 6x60s; Green 6x60s; Blue 6x60s.
  
• Measured effective Point Spread Function FWHM = 5.8 arcseconds, which on paper sounds pretty poor. 
• Processed from raw FITS images using my AstroPhotography python code (which uses astropy, photutils, ccdproc and Astrometry.net), some additional bash scripts, and Astromatic swarp (for resampling and co-addition) and stiff (for color image generation). No additional photoshop/gimp manipulation!